خوارزمية التعلم الآلي هي رمز برنامج (رياضيات أو منطق برنامج) يمكّن المحترفين من دراسة مجموعات البيانات الكبيرة المعقدة وتحليلها وفهمها واستكشافها. تشرح هذه المقالة أساسيات خوارزميات التعلم الآلي وتكشف عن أفضل 10 خوارزميات تعلم الآلة.
ما هي خوارزمية التعلم الآلي؟
تشير خوارزمية التعلم الآلي إلى رمز البرنامج (الرياضيات أو منطق البرنامج) الذي يمكّن المحترفين من دراسة مجموعات البيانات الكبيرة المعقدة وتحليلها وفهمها واستكشافها. تتبع كل خوارزمية سلسلة من التعليمات لتحقيق هدف إجراء تنبؤات أو تصنيف المعلومات عن طريق التعلم والتأسيس واكتشاف الأنماط المضمنة في البيانات.
ملاحظة: على الرغم من أن التعلم العميق هو مجال فرعي للتعلم الآلي ، إلا أنني لن أدرج أي خوارزميات التعلم العميق في هذا المنشور. أعتقد أنه يجب مناقشة خوارزميات التعلم العميق بشكل منفصل بسبب التعقيد وديناميكيات متميزة. إلى جانب ذلك ، أتردد في جعل هذا المنشور طويلاً للغاية وأتعب القراء.
أنواع التعلم الآلي
تحدد خوارزميات التعلم الآلي القواعد والعمليات التي يجب أن يأخذها النظام في الاعتبار أثناء معالجة مشكلة معينة. تقوم هذه الخوارزميات بتحليل ومحاكاة البيانات للتنبؤ بالنتيجة ضمن نطاق محدد مسبقًا.
علاوة على ذلك ، عندما يتم إدخال بيانات جديدة في هذه الخوارزميات ، فإنها تتعلم وتحسن وتحسن بناءً على التعليقات على الأداء السابق في توقع النتائج. بكلمات بسيطة ، تميل خوارزميات التعلم الآلي إلى أن تصبح "أكثر ذكاءً" مع كل تكرار.
اعتمادًا على نوع الخوارزمية ، تستخدم نماذج التعلم الآلي العديد من المعلمات مثل معلمة جاما ، والعمق الأقصى ، والجيران n ، وغيرها لتحليل البيانات وتحقيق نتائج دقيقة. هذه المعلمات هي نتيجة لبيانات التدريب التي تمثل مجموعة بيانات أكبر.
يتم تصنيف خوارزميات التعلم الآلي إلى أربعة أنواع بناءً على تقنيات التعلم: التعلم الخاضع للإشراف ، والشبه الخاضع للإشراف ، والتعلم غير الخاضع للإشراف ، والتعلم المعزز. تعد خوارزميات الانحدار والتصنيف أكثر الخيارات شيوعًا للتنبؤ بالقيم وتحديد أوجه التشابه واكتشاف أنماط البيانات غير العادية.

1.خوارزميات التعلم الخاضعة للإشراف
تستخدم خوارزميات التعلم الخاضعة للإشراف مجموعات بيانات معنونة لعمل تنبؤات. تكون تقنية التعلم هذه مفيدة عندما تعرف نوع النتيجة أو النتيجة التي تنوي الحصول عليها.
على سبيل المثال ، ضع في اعتبارك أن لديك مجموعة بيانات تحدد المطر الذي حدث في منطقة جغرافية خلال موسم معين على مدار الـ 200 عام الماضية. تنوي معرفة المطر المتوقع خلال هذا الموسم المحدد للسنوات العشر القادمة. هنا ، يتم اشتقاق النتيجة بناءً على الملصقات الموجودة في مجموعة البيانات الأصلية ، أي هطول الأمطار والمنطقة الجغرافية والموسم والسنة.
2.خوارزميات التعلم الغير خاضع للإشراف
تستخدم خوارزميات تعلم الآلة غير الخاضعة للإشراف بيانات غير مسماة. تقوم تقنية التعلم هذه بتسمية البيانات غير المسماة من خلال تصنيف البيانات أو التعبير عن نوعها أو شكلها أو هيكلها. تكون هذه التقنية مفيدة عندما يكون نوع النتيجة غير معروف.
على سبيل المثال ، عند استخدام مجموعة بيانات لمستخدمي Facebook ، فإنك تنوي تصنيف المستخدمين الذين يظهرون ميلًا (بناءً على الإعجابات) تجاه حملات إعلانية مماثلة على Facebook. في هذه الحالة ، تكون مجموعة البيانات غير مسماة. ومع ذلك ، ستحتوي النتيجة على تسميات حيث ستجد الخوارزمية أوجه تشابه بين نقاط البيانات أثناء تصنيف المستخدمين.
3.التعلم شبه الخاضع للإشراف (SSL)
تجمع خوارزميات التعلم شبه الخاضعة للإشراف بين الاثنين أعلاه ، حيث يتم استخدام البيانات المصنفة وغير المصنفة. الهدف من هذه الخوارزميات هو تصنيف البيانات غير المصنفة بناءً على المعلومات المستمدة من البيانات المصنفة.
ضع في اعتبارك مثال تصنيف محتوى الويب. يعتبر تصنيف وتصنيف المحتوى المتاح على الإنترنت مهمة تتطلب الكثير من الوقت والموارد. بصرف النظر عن خوارزميات الذكاء الاصطناعي ، يتطلب الأمر موارد بشرية لتنظيم مليارات صفحات الويب المتاحة عبر الإنترنت. في مثل هذه الحالات ، يمكن لنماذج التعلم شبه الخاضع للإشراف أن تلعب دورًا حاسمًا في إنجاز المهمة بكفاءة.
4.تعزيز التعلم
تستخدم خوارزميات التعلم المعزز النتيجة أو النتيجة كمعيار لتحديد خطوة العمل التالية. بمعنى آخر ، تتعلم هذه الخوارزميات من النتائج السابقة ، وتتلقى التعليقات بعد كل خطوة ، ثم تقرر ما إذا كانت ستمضي قدمًا في الخطوة التالية أم لا.
يتعلم النظام ما إذا كان قد اتخذ خيارًا صحيحًا أم خاطئًا أم محايدًا في هذه العملية. يمكن للأنظمة المؤتمتة أن تستخدم التعلم المعزز لأنها مصممة لاتخاذ القرارات بأقل قدر من التدخل البشري.
على سبيل المثال ، أنت تصمم سيارة ذاتية القيادة وتعتزم تتبع ما إذا كانت السيارة تتبع قواعد المرور وتضمن السلامة على الطرق. من خلال تطبيق التعلم المعزز ، تتعلم السيارة من خلال الخبرة وتكتيكات التعزيز. تضمن الخوارزمية أن السيارة تمتثل لقوانين المرور للبقاء في حارة واحدة ، وتتبع حدود السرعة ، وتتوقف عن مواجهة المشاة أو الحيوانات على الطريق.
أشهر خوارزميات التعلم الآلي
1.الانحدار الخطي
الانحدار الخطي هو خوارزمية تعلم خاضعة للإشراف وتحاول نمذجة العلاقة بين متغير هدف مستمر ومتغير واحد أو أكثر من المتغيرات المستقلة عن طريق ملاءمة معادلة خطية للبيانات.
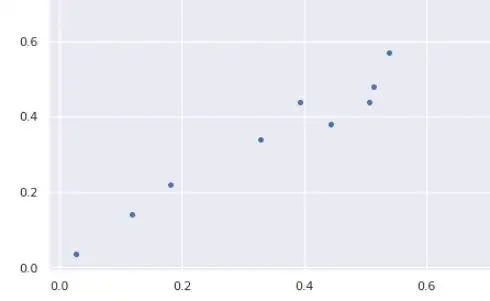
لكي يكون الانحدار الخطي اختيارًا جيدًا ، يجب أن تكون هناك علاقة خطية بين المتغير (المتغيرات) المستقلة والمتغير المستهدف. هناك العديد من الأدوات لاستكشاف العلاقة بين المتغيرات مثل مخططات التبعثر ومصفوفة الارتباط. على سبيل المثال ، يُظهر مخطط التبعثر أدناه ارتباطًا إيجابيًا بين متغير مستقل (محور س) ومتغير تابع (محور ص). كلما زاد أحدهما ، زاد الآخر أيضًا.
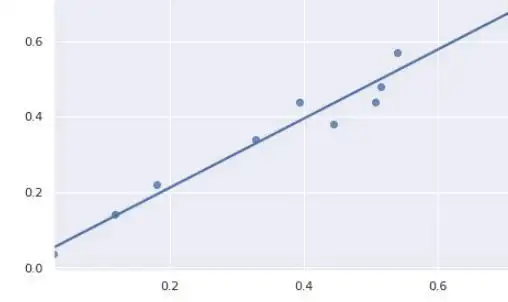
يحاول نموذج الانحدار الخطي ملاءمة خط الانحدار لنقاط البيانات التي تمثل العلاقات أو الارتباطات بشكل أفضل. الأسلوب الأكثر شيوعًا للاستخدام هو المربعات الصغرى العادية . باستخدام هذه الطريقة ، يتم العثور على أفضل خط انحدار عن طريق تقليل مجموع مربعات المسافة بين نقاط البيانات وخط الانحدار. بالنسبة لنقاط البيانات أعلاه ، يبدو خط الانحدار الذي تم الحصول عليه باستخدام المربعات الصغرى العادية كما يلي:
2.دعم آلة المتجهات SVM
تعد خوارزمية تعلم الآلة التي تسمى دعم آلة المتجهات Support Vector Machine عبارة عن خوارزمية تعليمية خاضعة للإشراف وتستخدم في الغالب لمهام التصنيف ولكنها مناسبة أيضًا لمهام الانحدار.
يميز دعم آلة المتجهات الفئات عن طريق رسم حدود القرار. تعد كيفية رسم أو تحديد حدود القرار الجزء الأكثر أهمية في خوارزميات دعم آلة المتجهات. قبل إنشاء حدود القرار ، يتم رسم كل ملاحظة (أو نقطة بيانات) في مساحة ذات أبعاد n.
. n هو عدد الميزات المستخدمة. على سبيل المثال ، إذا استخدمنا "الطول" و "العرض" لتصنيف "خلايا" مختلفة ، يتم رسم الملاحظات في فضاء ثنائي الأبعاد وحدود القرار عبارة عن خط. إذا استخدمنا 3 ميزات ، فإن حدود القرار هي مستوى في مساحة ثلاثية الأبعاد. إذا استخدمنا أكثر من 3 ميزات ، تصبح حدود القرار مستويًا مفرطًا يصعب تخيله حقًا.
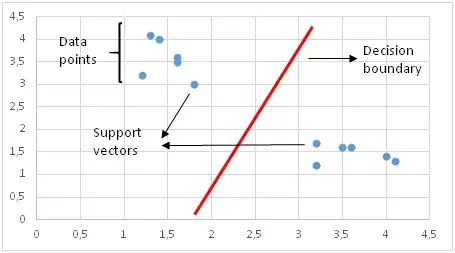
يتم رسم حدود القرار بطريقة يتم فيها تكبير المسافة إلى نواقل الدعم. إذا كانت حدود القرار قريبة جدًا من متجه الدعم ، فستكون حساسة للغاية للضوضاء ولن يتم تعميمها بشكل جيد. حتى التغييرات الصغيرة جدًا في المتغيرات المستقلة قد تتسبب في سوء تصنيف.
لا يمكن دائمًا فصل نقاط البيانات خطيًا كما في الشكل أعلاه. في هذه الحالات ، يستخدم دعم آلة المتجهات دالة kernel التي تقيس تشابه (أو قرب) نقاط البيانات في مساحة ذات أبعاد أعلى من أجل جعلها قابلة للفصل خطيًا.
دالة Kernel هي نوع من قياس التشابه. المدخلات هي ميزات أصلية والمخرج هو مقياس تشابه في مساحة الميزة الجديدة. التشابه هنا يعني درجة من التقارب. إنها عملية مكلفة لتحويل نقاط البيانات فعليًا إلى مساحة ميزة عالية الأبعاد.
لا تقوم الخوارزمية في الواقع بتحويل نقاط البيانات إلى مساحة ميزة جديدة عالية الأبعاد. يحسب دعم آلة المتجهات الموجه محو النواة Kernelized SVM حدود القرار من حيث مقاييس التشابه في مساحة ميزة عالية الأبعاد دون إجراء تحويل فعليًا. أعتقد أن هذا هو السبب في أنها تسمى أيضًا خدعة النواة.
يعد دعم آلة المتجهات فعالًا بشكل خاص في الحالات التي يكون فيها عدد الأبعاد أكبر من عدد العينات. عند العثور على حدود القرار ، يستخدم دعم آلة المتجهات مجموعة فرعية من نقاط التدريب بدلاً من جميع النقاط مما يجعل الذاكرة فعالة. من ناحية أخرى ، يزيد وقت التدريب لمجموعات البيانات الكبيرة مما يؤثر سلبًا على الأداء.
3.تصنيف Naive Bayes
Naive Bayes هي خوارزمية تعلم خاضعة للإشراف تستخدم لمهام التصنيف. ومن ثم ، يطلق عليه أيضًا اسم Naive Bayes Classifier.
يفترض Naive bayes أن الميزات مستقلة عن بعضها البعض ولا يوجد ارتباط بين الميزات. ومع ذلك ، هذا ليس هو الحال في الحياة الحقيقية. هذا الافتراض الساذج للميزات غير المترابطة هو سبب تسمية هذه الخوارزمية بـ "السذاجة".
الحدس وراء خوارزمية بايز الساذجة هو نظرية بايز:
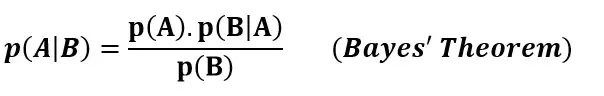
p (A | B): احتمالية وقوع الحدث A حدث معين B قد وقع بالفعل
p (B | A): احتمالية الحدث B نظرًا للحدث A الذي حدث بالفعل
p(A): احتمالية الحدث A
p(B): احتمالية الحدث B
يحسب المصنف Naive bayes احتمال فئة معينة بمجموعة من قيم الميزة (على سبيل المثال ، p (yi | x1 ، x2 ، … ، xn)). أدخل هذا في نظرية بايز:
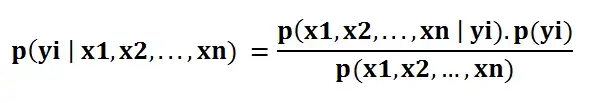
تعني p (x1، x2، …، xn | yi) احتمال وجود مجموعة معينة من الميزات (ملاحظة / صف في مجموعة بيانات) مع إعطاء تصنيف للفئة. نحتاج إلى مجموعات بيانات كبيرة للغاية للحصول على تقدير للتوزيع الاحتمالي لجميع المجموعات المختلفة لقيم الميزات. للتغلب على هذه المشكلة ، تفترض خوارزمية بايز الساذجة أن جميع الميزات مستقلة عن بعضها البعض.
علاوة على ذلك ، يمكن إزالة المقام (p (x1 ، x2 ، … ، xn)) لتبسيط المعادلة لأنها تقوم فقط بتطبيع قيمة الاحتمال الشرطي لفئة معينة عند الملاحظة (p (yi | x1 ، x2 ، … ، xn) ).
من السهل جدًا حساب احتمال وجود فئة (p (yi)):

في ظل افتراض أن الميزات مستقلة ، يمكن كتابة p (x1، x2، …، xn | yi) على النحو التالي:
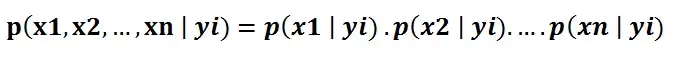
يمكن تقدير الاحتمال الشرطي لميزة واحدة مع مراعاة تسمية الفئة (أي p (x1 | yi)) بسهولة أكبر من البيانات. تحتاج الخوارزمية إلى تخزين التوزيعات الاحتمالية للميزات لكل فئة بشكل مستقل. على سبيل المثال ، إذا كان هناك 5 فئات و 10 ميزات ، فيجب تخزين 50 توزيعًا احتماليًا مختلفًا.
بعد جمع كل هذه الأمور ، أصبح من السهل لخوارزمية بايز الساذجة حساب احتمالية ملاحظة فئة معينة من قيم الميزات (p (yi | x1 ، x2 ، … ، xn))
الافتراض بأن جميع الميزات مستقلة يجعل خوارزمية بايز الساذجة سريعة جدًا مقارنة بالخوارزميات المعقدة. في بعض الحالات ، تُفضل السرعة على الدقة العالية. من ناحية أخرى ، فإن نفس الافتراض يجعل خوارزمية بايز الساذجة أقل دقة من الخوارزميات المعقدة. السرعة تأتي بتكلفة!
أنظر أيضاً:
4.الانحدار اللوجستي
الانحدار اللوجستي هو خوارزمية تعلم خاضعة للإشراف والتي تستخدم في الغالب لمشاكل التصنيف الثنائي. على الرغم من أن "الانحدار" يتعارض مع "التصنيف" ، إلا أن التركيز هنا ينصب على كلمة "لوجيستي" التي تشير إلى الوظيفة اللوجيستية التي تقوم بمهمة التصنيف في هذه الخوارزمية.
الانحدار اللوجستي عبارة عن خوارزمية تصنيف بسيطة لكنها فعالة للغاية ، لذا فهي تستخدم بشكل شائع للعديد من مهام التصنيف الثنائي. يعد اضطراب العملاء أو البريد الإلكتروني العشوائي أو موقع الويب أو تنبؤات النقر فوق الإعلان بعض الأمثلة على المجالات التي يقدم فيها الانحدار اللوجستي حلاً فعالاً.
أساس الانحدار اللوجستي هو الوظيفة اللوجيستية ، والتي تسمى أيضًا الوظيفة السينية ، والتي تأخذ أي رقم ذي قيمة حقيقية وتعيينه إلى قيمة بين 0 و 1.
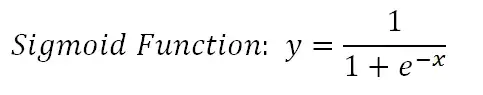
ضع في اعتبارك أن لدينا المعادلة الخطية التالية لحلها:
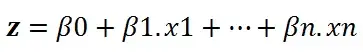
يأخذ نموذج الانحدار اللوجستي معادلة خطية كمدخلات ويستخدم وظيفة لوجستية وتسجيل احتمالات لأداء مهمة تصنيف ثنائي. بعد ذلك ، سوف نحصل على الرسم البياني الشهير على شكل s للانحدار اللوجستي:
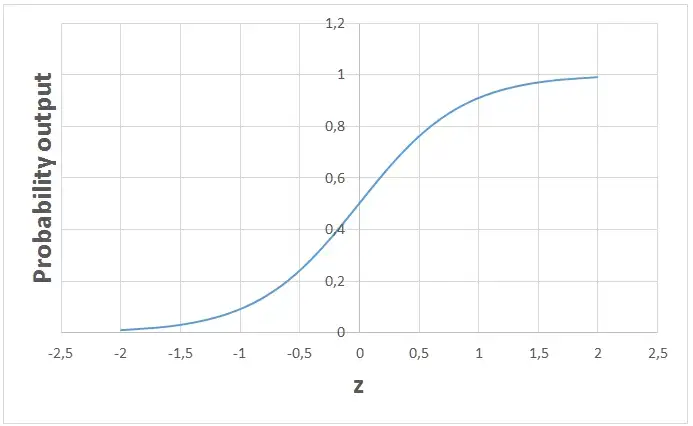
يمكننا استخدام الاحتمال المحسوب "كما هو". على سبيل المثال ، يمكن أن يكون الناتج "احتمال أن يكون هذا البريد الإلكتروني بريدًا عشوائيًا بنسبة 95٪" أو "احتمال أن ينقر العميل على هذا الإعلان هو 70٪". ومع ذلك ، في معظم الحالات ، يتم استخدام الاحتمالات لتصنيف نقاط البيانات. على سبيل المثال ، إذا كان الاحتمال أكبر من 50٪ ، فإن التوقع هو فئة موجبة (1). خلاف ذلك ، يكون التوقع فئة سالبة (0).
ليس من المرغوب دائمًا اختيار فئة موجبة لجميع قيم الاحتمالات الأعلى من 50٪. فيما يتعلق بقضية البريد الإلكتروني العشوائي ، يجب أن نكون على يقين تقريبًا من أجل تصنيف البريد الإلكتروني على أنه بريد عشوائي.
نظرًا لأن رسائل البريد الإلكتروني التي تم اكتشافها كرسائل غير مرغوب فيها تنتقل مباشرة إلى مجلد البريد العشوائي ، فإننا لا نريد أن يفوت المستخدم رسائل البريد الإلكتروني المهمة. لا يتم تصنيف رسائل البريد الإلكتروني على أنها بريد عشوائي إلا إذا كنا متأكدين تقريبًا. من ناحية أخرى ، عندما يتطلب التصنيف في مسألة متعلقة بالصحة أن نكون أكثر حساسية. حتى لو كنا نشك قليلاً في أن الخلية خبيثة ، فنحن لا نريد أن نفوتها.
لذا فإن القيمة التي تعمل كعتبة بين الصنف الموجب والسالب تعتمد على المشكلة. الشيء الجيد هو أن الانحدار اللوجستي يسمح لنا بضبط هذه القيمة الحدية.
5.ﺨﻭﺍﺭﺯﻤﻴﺔ ﺍﻟﺠﺎﺭ ﺍﻷﻗﺭﺏ (kNN)
ﺨﻭﺍﺭﺯﻤﻴﺔ ﺍﻟﺠﺎﺭ ﺍﻷﻗﺭﺏ عبارة عن خوارزمية تعلم خاضعة للإشراف يمكن استخدامها لحل كل من مهام التصنيف والانحدار. الفكرة الرئيسية وراء ﺨﻭﺍﺭﺯﻤﻴﺔ ﺍﻟﺠﺎﺭ ﺍﻷﻗﺭﺏ هي أن قيمة أو صنف نقطة البيانات يتم تحديدها من خلال نقاط البيانات حولها.
يحدد مصنف ﺨﻭﺍﺭﺯﻤﻴﺔ ﺍﻟﺠﺎﺭ ﺍﻷﻗﺭﺏ فئة نقطة البيانات من خلال مبدأ تصويت الأغلبية. على سبيل المثال ، إذا تم ضبط k على 5 ، يتم فحص فئات أقرب 5 نقاط. يتم التنبؤ وفقًا لفئة الأغلبية. وبالمثل ، يأخذ انحدار ﺨﻭﺍﺭﺯﻤﻴﺔ ﺍﻟﺠﺎﺭ ﺍﻷﻗﺭﺏ القيمة المتوسطة لأقرب 5 نقاط. دعونا نلقي نظرة على مثال. ضع في اعتبارك نقاط البيانات التالية التي تنتمي إلى 4 فئات مختلفة:
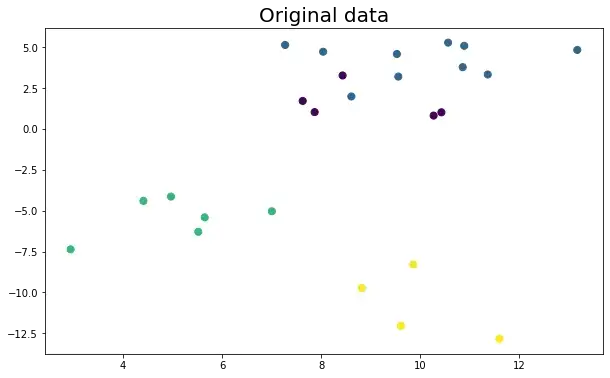
دعونا نرى كيف تتغير الفئات المتوقعة وفقًا لقيمة k:
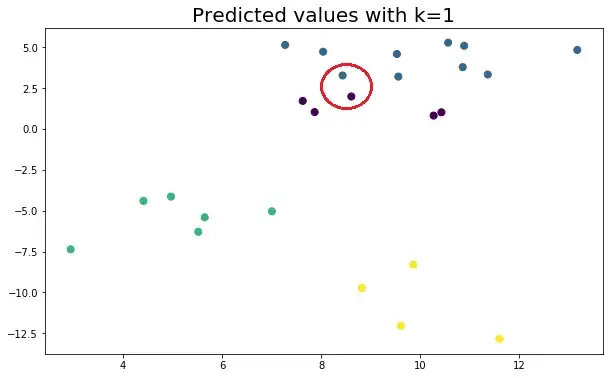
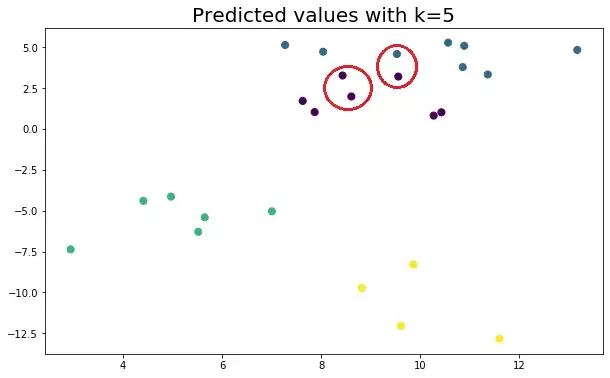
من المهم جدًا تحديد قيمة k المثلى. إذا كان k منخفضًا جدًا ، يكون النموذج محددًا جدًا ولا يتم تعميمه جيدًا. كما أنها تميل إلى أن تكون حساسة للضوضاء. يحقق النموذج دقة عالية في مجموعة القطار ولكنه سيكون مؤشرًا ضعيفًا على نقاط البيانات الجديدة التي لم تتم رؤيتها من قبل.
لذلك ، من المحتمل أن ينتهي بنا الأمر بنموذج إضافي. من ناحية أخرى ، إذا كان k كبيرًا جدًا ، فسيكون النموذج معممًا جدًا وليس مؤشرًا جيدًا في كل من مجموعات القطار والاختبار. يُعرف هذا الوضع بالنقص المناسب.
ﺨﻭﺍﺭﺯﻤﻴﺔ ﺍﻟﺠﺎﺭ ﺍﻷﻗﺭﺏ بسيط وسهل التفسير. لا يقوم بأي افتراض لذلك يمكن تنفيذه في المهام غير الخطية. تصبح ﺨﻭﺍﺭﺯﻤﻴﺔ ﺍﻟﺠﺎﺭ ﺍﻷﻗﺭﺏ بطيئة للغاية مع زيادة عدد نقاط البيانات لأن النموذج يحتاج إلى تخزين جميع نقاط البيانات. وبالتالي ، فهي أيضًا ليست فعالة في الذاكرة. الجانب السلبي الآخر لـﺨﻭﺍﺭﺯﻤﻴﺔ ﺍﻟﺠﺎﺭ ﺍﻷﻗﺭﺏ هو أنه حساس للقيم المتطرفة.
أنظر أيضاً: ما هي لغة جافا؟
6. خوارزمية أشجار القرار
هي إحدى أشهر خوارزميات التعلم الآلي و تعتمد على طرح الأسئلة بشكل متكرر لتقسيم البيانات. من الأسهل تصور تقسيم البيانات بتمثيل مرئي لشجرة القرار:
يمثل هذا شجرة قرار للتنبؤ بضخ العميل. يعتمد التقسيم الأول على مبلغ الرسوم الشهرية. ثم تستمر الخوارزمية في طرح الأسئلة لفصل تسميات الفصل. تصبح الأسئلة أكثر تحديدًا كلما تعمقت الشجرة.
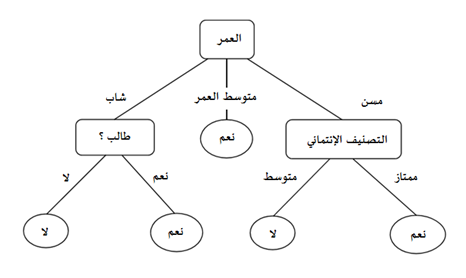
الهدف من خوارزمية شجرة القرار هو زيادة القدرة على التنبؤ بأكبر قدر ممكن في كل قسم بحيث يستمر النموذج في الحصول على معلومات حول مجموعة البيانات. لا يمنحنا تقسيم الميزات عشوائيًا في العادة نظرة ثاقبة لمجموعة البيانات.
تكون الانقسامات التي تزيد من نقاء العقد أكثر إفادة. يتناسب نقاء العقدة عكسيا مع توزيع الفئات المختلفة في تلك العقدة. فالأسئلة التي يجب طرحها تنتقي على نحو يزيد الطهارة أو ينقص النجاسة.
كم عدد الأسئلة التي نسألها؟ متى نتوقف؟ متى تكون شجرتنا كافية لحل مشكلة التصنيف؟ تقودنا الإجابة على كل هذه الأسئلة إلى أحد أهم المفاهيم في التعلم الآلي: التجهيز الزائد. يمكن للنموذج الاستمرار في طرح الأسئلة حتى تصبح جميع العقد نقية.
ومع ذلك ، سيكون هذا نموذجًا محددًا للغاية ولن يتم تعميمه جيدًا. يحقق دقة عالية مع مجموعة التدريب ولكنه يؤدي بشكل ضعيف على نقاط البيانات الجديدة التي لم تتم رؤيتها من قبل مما يشير إلى التجهيز الزائد. يتم التحكم في عمق الشجرة بواسطة معلمة max_depth لخوارزمية شجرة القرار في scikit-Learn.
لا تتطلب خوارزمية شجرة القرار عادةً تطبيع الميزات أو قياسها. كما أنه مناسب للعمل على مزيج من أنواع بيانات المعالم (مستمر ، فئوي ، ثنائي). على الجانب السلبي ، فهو عرضة للتركيب الزائد ويحتاج إلى التجميع من أجل التعميم بشكل جيد.
7.الغابة العشوائية
الغابة العشوائية عبارة عن مجموعة من العديد من أشجار القرار. يتم إنشاء الغابات العشوائية باستخدام طريقة تسمى التعبئة في أكياس يتم فيها استخدام أشجار القرار كمقدرات موازية. إذا تم استخدامها لمشكلة تصنيف ، تعتمد النتيجة على تصويت الأغلبية للنتائج الواردة من كل شجرة قرار.
بالنسبة للانحدار ، فإن توقع العقدة الطرفية هو القيمة المتوسطة للقيم المستهدفة في تلك الصفحة. يأخذ الانحدار العشوائي للغابات قيمة متوسطة للنتائج من أشجار القرار.
تقلل الغابات العشوائية من خطر التجهيز الزائد والدقة أعلى بكثير من شجرة قرار واحدة. علاوة على ذلك ، تعمل أشجار القرار في غابة عشوائية بالتوازي بحيث لا يصبح الوقت عنق زجاجة.
يعتمد نجاح الغابة العشوائية بشكل كبير على استخدام أشجار القرار غير المرتبطة. إذا استخدمنا أشجارًا متشابهة أو متشابهة جدًا ، فلن تختلف النتيجة الإجمالية كثيرًا عن نتيجة شجرة قرار واحدة. تحقق الغابات العشوائية وجود أشجار قرار غير مرتبطة عن طريق التمهيد والعشوائية المميزة.
Bootstrapping أو ما نسميه بــ طريق التمهيد هو اختيار عشوائي لعينات من بيانات التدريب مع الاستبدال. يطلق عليهم عينات التمهيد.
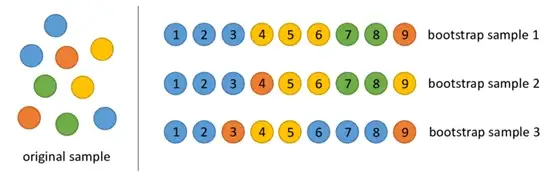
يتم تحقيق عشوائية الميزة عن طريق تحديد الميزات عشوائيًا لكل شجرة قرار في مجموعة تفرعات عشوائية. يمكن التحكم في عدد الميزات المستخدمة لكل شجرة في غابة عشوائية باستخدام معلمة max_features.

تعد Random Forest نموذجًا عالي الدقة في العديد من المشكلات المختلفة ولا تتطلب تطبيعًا أو تحجيمًا. ومع ذلك ، فهو ليس اختيارًا جيدًا لمجموعات البيانات عالية الأبعاد (أي تصنيف النص) مقارنة بالنماذج الخطية السريعة (مثل بايز Naive).
أنظر أيضاً: تطبيقات الذكاء الإصطناعي
8.أشجار القرار المعزز بالتدرج (GBDT)
أشجار القرار المعزز بالتدرج عبارة عن خوارزمية تعلم آلي تجميعية تستخدم طريقة التعزيز لدمج أشجار القرار الفردية.
التعزيز يعني الجمع بين خوارزمية التعلم في سلسلة لتحقيق متعلم قوي من العديد من المتعلمين الضعفاء المتصلين بالتتابع. في حالة أشجار القرار المعزز بالتدرج، فإن المتعلمين الضعفاء هم أشجار القرار.
تحاول كل شجرة تقليل أخطاء الشجرة السابقة. تعتبر الأشجار في التعزيز من المتعلمين الضعفاء ولكن إضافة العديد من الأشجار في سلسلة وكل منها يركز على الأخطاء من سابقتها يجعل تعزيز نموذج عالي الكفاءة والدقة. على عكس التعبئة ، لا يتضمن التعزيز أخذ عينات التمهيد. في كل مرة يتم فيها إضافة شجرة جديدة ، فإنها تناسب نسخة معدلة من مجموعة البيانات الأولية.
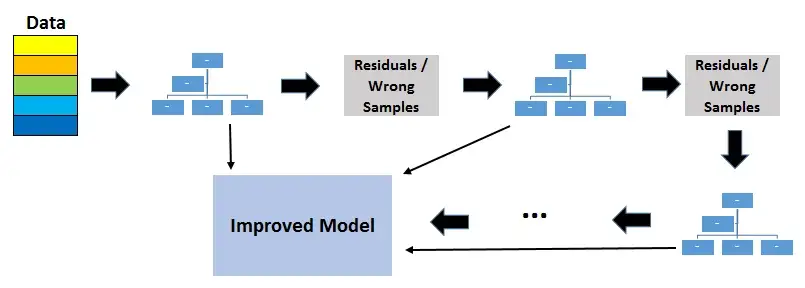
نظرًا لأنه يتم إضافة الأشجار بالتتابع ، فإن تعزيز الخوارزميات تتعلم ببطء. في التعلم الإحصائي ، تعمل النماذج التي تتعلم ببطء بشكل أفضل.
يتم استخدام وظيفة الخسارة لاكتشاف المخلفات. على سبيل المثال ، يمكن استخدام الخطأ التربيعي المتوسط (MSE) لمهمة الانحدار ويمكن استخدام الخسارة اللوغاريتمية (فقدان السجل) لمهام التصنيف. تجدر الإشارة إلى أن الأشجار الموجودة في النموذج لا تتغير عند إضافة شجرة جديدة. تناسب شجرة القرار المضافة القيم المتبقية من النموذج الحالي.
معدل التعلم و n_estimators هما معلمات تشعبية بالغة الأهمية لتعزيز التدرج اللوني لأشجار القرار. معدل التعلم ، المشار إليه بـ α ، يعني ببساطة مدى سرعة تعلم النموذج. كل شجرة جديدة تعدل النموذج العام. يتم التحكم في حجم التعديل من خلال معدل التعلم.
n_estimator هو عدد الأشجار المستخدمة في النموذج. إذا كان معدل التعلم منخفضًا ، فنحن بحاجة إلى المزيد من الأشجار لتدريب النموذج. ومع ذلك ، يجب أن نكون حذرين للغاية في اختيار عدد الأشجار. إنه يخلق مخاطر عالية من التجهيز المفرط لاستخدام الكثير من الأشجار.
تعتبر أشجار القرار المعزز بالتدرج فعالة للغاية في مهام التصنيف والانحدار وتوفر تنبؤات أكثر دقة مقارنة بالغابات العشوائية. يمكنه التعامل مع نوع مختلط من الميزات وليس هناك حاجة إلى معالجة مسبقة. تتطلب أشجار القرار المعزز بالتدرج ضبطًا دقيقًا للمعلمات الفائقة من أجل منع النموذج من التجهيز الزائد.
تعد خوارزمية أشجار القرار المعزز بالتدرج قوية جدًا لدرجة أنه تم تنفيذ العديد من الإصدارات التي تمت ترقيتها مثل XGBOOST و LightGBM و CatBoost.
ملاحظة على overfitting
يتمثل أحد الاختلافات الرئيسية بين الغابات العشوائية وأشجار القرار التي تعزز التدرج في عدد الأشجار المستخدمة في النموذج. زيادة عدد الأشجار في الغابات العشوائية لا يسبب فرط التجهيز. بعد نقطة معينة ، لا تزداد دقة النموذج بإضافة المزيد من الأشجار ، ولكنها أيضًا لا تتأثر سلبًا بإضافة أشجار زائدة.
ما زلت لا ترغب في إضافة كمية غير ضرورية من الأشجار لأسباب حسابية ولكن لا يوجد خطر من التخصيص المرتبط بعدد الأشجار في الغابات العشوائية.
ومع ذلك ، فإن عدد الأشجار في التدرج الذي يعزز أشجار القرار أمر بالغ الأهمية من حيث التجهيز الزائد. ستؤدي إضافة الكثير من الأشجار إلى فرط التجهيز ، لذا من المهم التوقف عن إضافة الأشجار في وقت ما.
9.K-Means Clustering
كإحدى أشهر خوارزميات التعلم الآلي ، تعتبر خوارزمية متوسط التجميع هو طريقة لتجميع مجموعة من نقاط البيانات بطريقة يتم فيها تجميع نقاط البيانات المتشابهة معًا. لذلك ، تبحث خوارزميات التجميع عن أوجه التشابه أو الاختلاف بين نقاط البيانات. التجميع هو طريقة تعلم غير خاضعة للإشراف ، لذا لا توجد تسمية مرتبطة بنقاط البيانات. تحاول خوارزميات التجميع إيجاد البنية الأساسية للبيانات.
ملاحظة: التجميع ليس تصنيفًا.
الملاحظات (أو نقاط البيانات) في مهمة التصنيف لها تسميات. يتم تصنيف كل ملاحظة حسب بعض القياسات. تحاول خوارزميات التصنيف نمذجة العلاقة بين القياسات (الميزات) في الملاحظات والفئة المخصصة لها. ثم يتنبأ النموذج بفئة الملاحظات الجديدة.
تهدف K-mean clustering إلى تقسيم البيانات إلى مجموعات k بطريقة تتشابه فيها نقاط البيانات في نفس المجموعة وتكون نقاط البيانات في المجموعات المختلفة متباعدة. وبالتالي ، فهي تقنية تجميع قائمة على التقسيم. يتم تحديد التشابه بين نقطتين من خلال المسافة بينهما.
يحاول التجميع K-mean clustering تقليل المسافات داخل الكتلة وزيادة المسافة بين المجموعات المختلفة. خوارزمية K-mean غير قادرة على تحديد عدد المجموعات. نحتاج إلى تعريفه عند إنشاء كائن KMeans والذي قد يكون مهمة صعبة.
ضع في اعتبارك التصور ثنائي الأبعاد التالي لمجموعة البيانات:

يمكن تقسيمها إلى 4 مجموعات مختلفة على النحو التالي:

تعتبر مجموعات البيانات الواقعية أكثر تعقيدًا بكثير حيث لا يتم فصل المجموعات بوضوح. ومع ذلك ، فإن الخوارزمية تعمل بنفس الطريقة. K- الوسائل هي عملية تكرارية. إنه مبني على خوارزمية تعظيم التوقع. بعد تحديد عدد الكتل ، يتم العمل من خلال تنفيذ الخطوات التالية:
- اختيار النقط الوسطى عشوائيا (مركز الكتلة) لكل مجموعة.
- احسب مسافة جميع نقاط البيانات إلى النقطه الوسطى.
- قم بتعيين نقاط البيانات إلى أقرب مجموعة.
- ابحث عن النقط الوسطى الجديدة لكل مجموعة عن طريق أخذ متوسط جميع نقاط البيانات في المجموعة.
كرر الخطوتين 2 و 3 و 4 حتى تتقارب جميع النقاط وتتوقف مراكز المجموعة عن الحركة.
يعتبر تجميع K-Means سريعة نسبيًا وسهلة التفسير. كما أنه قادر على اختيار مواضع النقط الوسطى الأولية بطريقة ذكية تسرع التقارب.
أحد التحديات التي تواجهها مع الوسائل k هو أن عدد المجموعات يجب أن يكون محددًا مسبقًا. خوارزمية K-mean غير قادرة على تخمين عدد المجموعات الموجودة في البيانات. إذا كان هناك بنية غير خطية تفصل بين المجموعات في البيانات ، فلن تكون الوسائل k اختيارًا جيدًا.
10.المجموعات الهرمية
يعني التجميع الهرمي إنشاء شجرة من المجموعات عن طريق تجميع نقاط البيانات أو فصلها بشكل متكرر. هناك نوعان من المجموعات الهرمية:
- التكتل العنقودي
- المجموعات الانقسامية
تتمثل إحدى مزايا التجميع الهرمي في أنه لا يتعين علينا تحديد عدد المجموعات (ولكن يمكننا ذلك).
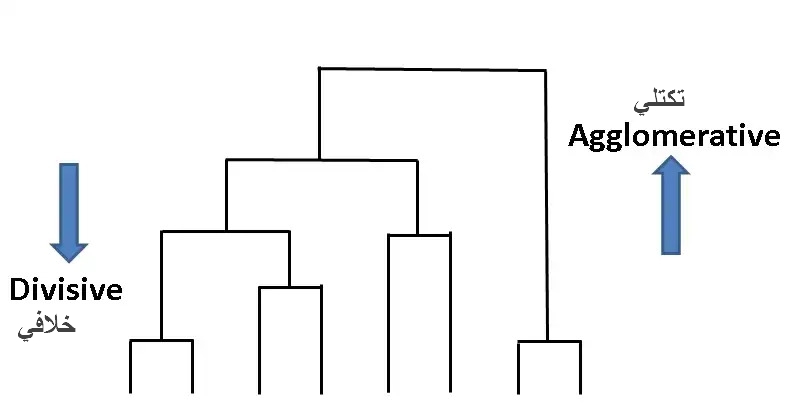
التكتل العنقودي هو نوع من النهج التصاعدي. من المفترض أن تكون كل نقطة بيانات مجموعة منفصلة في البداية. ثم يتم دمج المجموعات المتشابهة بشكل متكرر.
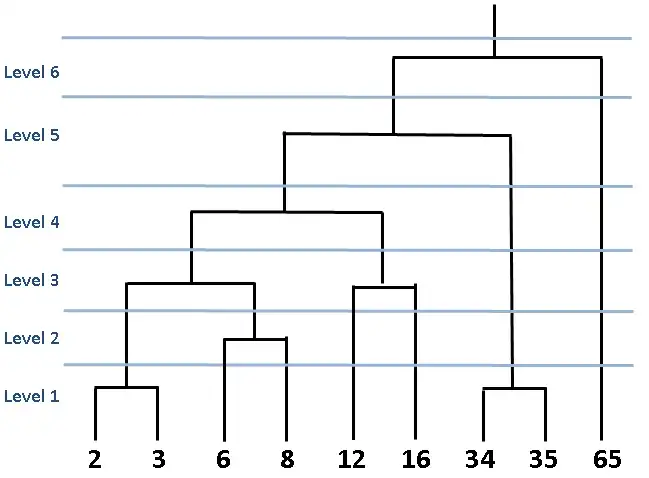
الشكل أعلاه يسمى dendrogram وهو رسم تخطيطي يمثل النهج القائم على الشجرة. في المجموعات الهرمية ، تُستخدم مخططات التخطيط لتصور العلاقة بين المجموعات.
تتمثل إحدى مزايا التجميع الهرمي في أنه لا يتعين علينا تحديد عدد المجموعات مسبقًا. ومع ذلك ، ليس من الحكمة دمج جميع نقاط البيانات في مجموعة واحدة. يجب أن نتوقف عن دمج المجموعات في مرحلة ما. يوفر Scikit-Learn خيارين لهذا:
- توقف بعد الوصول إلى عدد من المجموعات (n_clusters)
- قم بتعيين قيمة حدية للربط (المسافة_الحد). إذا كانت المسافة بين مجموعتين أعلى من الحد الأدنى ، فلن يتم دمج هذه المجموعات.
لا تُستخدم المجموعات الانقسامية بشكل شائع في الحياة الواقعية ، لذا سأذكرها باختصار. التفسير البسيط والواضح هو أن التجمعات الخلافية هي عكس التجمعات التراكمية. نبدأ بمجموعة عملاقة واحدة تشمل جميع نقاط البيانات. ثم يتم فصل نقاط البيانات إلى مجموعات مختلفة. إنه نهج يصل إلى أسفل.
تقوم المجموعات الهرمية دائمًا بإنشاء نفس المجموعات. قد ينتج عن متوسط التجميع K-means clustering مجموعات مختلفة اعتمادًا على كيفية بدء النقط الوسطى (مركز الكتلة). ومع ذلك ، فهي خوارزمية أبطأ مقارنة بالوسائل k. يستغرق التجميع الهرمي وقتًا طويلاً للتشغيل خاصة لمجموعات البيانات الكبيرة.
اختيار أفضل خوارزمية لك
كمبتدئ ، قد تحتاج إلى مساعدة في تسوية أفضل خوارزمية. يمثل هذا القرار تحديًا في عالم مليء بالخيارات الرائعة. ومع ذلك ، في البداية ، يجب أن تبني اختيارك على شيء آخر غير الميزات الرائعة للخوارزمية.
بدلاً من ذلك ، يجب أن تفكر في حجم الخوارزمية وطبيعة البيانات وإلحاح المهام ومتطلبات الأداء. ستساعدك هذه العوامل ، من بين أمور أخرى ، على التأكد من الخوارزمية المثالية لمشروعك.
خلاصة
تميل خوارزميات التعلم الآلي إلى التعلم من الملاحظات. يقومون بتحليل البيانات ، تعيين المدخلات للمخرجات ، واكتشاف أنماط البيانات. تصبح الخوارزميات أكثر ذكاءً لأنها تعالج المزيد من البيانات ، مما يحسن الأداء التنبئي العام.
اعتمادًا على المتطلبات المتغيرة وتعقيد المشكلات ، تستمر المتغيرات الجديدة لخوارزميات التعلم الآلي الحالية في الظهور. يمكنك اختيار الخوارزمية التي تناسب احتياجاتك على أفضل وجه والحصول على السبق في التعلم الآلي.