ما هو معامل الارتباط في الإحصاء ؟ وكيف يتم حسابه ؟ مع أمثلة

يستخدم معامل الارتباط في الإحصاء لقياس مدى قوة العلاقة بين متغيرين. هناك عدة أنواع من معامل الارتباط في الإحصاء ، ولكن الأكثر شيوعًا هو معامل بيرسون. ارتباط بيرسون (ويسمى أيضًا Pearson’s R) هو معامل ارتباط شائع الاستخدام في الانحدار الخطي.

إذا كنت بدأت للتو في مجال الإحصاء ، فمن المحتمل أن تتعرف على معامل الارتباط Pearson’s R أولاً. في الواقع ، عندما يشير أي شخص إلى معامل الارتباط ، فإنه يتحدث عادة عن معامل بيرسون.

ما هو الارتباط؟

الارتباط هو مقياس إحصائي للعلاقة بين متغيرين. من الأفضل استخدام المقياس في المتغيرات التي توضح علاقة خطية بين بعضها البعض. يمكن تمثيل ملاءمة البيانات بشكل مرئي في مخطط مبعثر. باستخدام مخطط التشتت ، يمكننا بشكل عام تقييم العلاقة بين المتغيرات وتحديد ما إذا كانت مترابطة أم لا.

ما هو معامل الارتباط في الإحصاء؟

معامل الارتباط هو المقياس المحدد الذي يحدد قوة العلاقة الخطية بين متغيرين في تحليل الارتباط. المعامل هو ما نرمز إليه بـ r في تقرير الارتباط.

معامل الارتباط r قيمة خالية من الوحدات بين -1 و 1. يشار إلى الدلالة الإحصائية بقيمة p. لذلك ، تُكتب الارتباطات عادةً برقمين رئيسيين: r = و p =.

• كلما اقترب r من الصفر ، كانت العلاقة الخطية أضعف.
• تشير قيم r الموجبة إلى ارتباط موجب ، حيث تميل قيم كلا المتغيرين إلى الزيادة معًا.
• تشير قيم r السالبة إلى ارتباط سلبي ، حيث تميل قيم أحد المتغيرات إلى الزيادة عندما تنخفض قيم المتغير الآخر.
• تمثل القيمتان 1 و -1 ارتباطات “كاملة” ، إيجابية وسلبية على التوالي. متغيرين مترابطين تمامًا يتغيران معًا بمعدل ثابت. نقول أن لديهم علاقة خطية ؛ عند رسمها على مخطط مبعثر ، يمكن توصيل جميع نقاط البيانات بخط مستقيم.
• تساعدنا القيمة p على تحديد ما إذا كان بإمكاننا الاستنتاج بشكل مفيد أن معامل ارتباط السكان يختلف عن الصفر ، بناءً على ما نلاحظه من العينة.

ماذا يخبرك معامل الارتباط في الإحصاء ؟

تلخص معاملات الارتباط البيانات وتساعدك على مقارنة النتائج بين الدراسات.

تلخيص البيانات

معامل الارتباط هو إحصاء وصفي. هذا يعني أنه يلخص بيانات العينة دون السماح لك باستنتاج أي شيء عن السكان. معامل الارتباط هو إحصاء ثنائي المتغير عندما يلخص العلاقة بين متغيرين ، ويكون إحصائيًا متعدد المتغيرات عندما يكون لديك أكثر من متغيرين.

إذا كان معامل الارتباط الخاص بك يعتمد على بيانات نموذجية ، فستحتاج إلى إحصائية استنتاجية إذا كنت تريد تعميم نتائجك على السكان. يمكنك استخدام اختبار F أو اختبار t لحساب إحصاء اختبار يخبرك بالأهمية الإحصائية لاكتشافك.

مقارنة الدراسات

معامل الارتباط في الإحصاء هو أيضًا مقياس حجم التأثير ، والذي يخبرك بالأهمية العملية للنتيجة.

معاملات الارتباط خالية من الوحدات ، مما يجعل من الممكن مقارنة المعاملات مباشرة بين الدراسات.

كيف يتم استخدام معامل الارتباط؟

بالنسبة لمتغيرين ، تقارن الصيغة مسافة كل نقطة بيانات من المتوسط المتغير وتستخدم هذا لإخبارنا بمدى ملاءمة العلاقة بين المتغيرات لخط وهمي مرسوم من خلال البيانات. هذا ما نعنيه عندما نقول أن الارتباطات تنظر إلى العلاقات الخطية.

أنظر أيضاً: أنواع المتغيرات الإحصائية

كيف نحسب بالفعل معامل الارتباط؟

يمكن تمثيل معامل ارتباط العينة بالصيغة التالية:

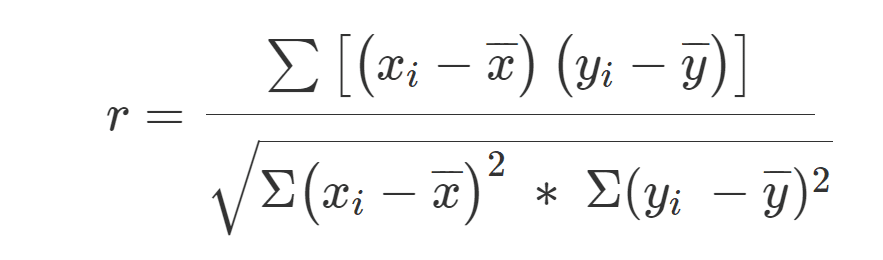
دعنا ننتقل إلى كيفية حساب معامل الارتباط باستخدام مثال مع مجموعة صغيرة من الأرقام البسيطة ، بحيث يكون من السهل متابعة العمليات.

لنتخيل أننا مهتمون بما إذا كان بإمكاننا توقع زيادة مبيعات الآيس كريم في مدينتنا في الأيام الحارة. تبدأ محلات الآيس كريم في الافتتاح في الربيع. ربما يشتري الناس المزيد من الآيس كريم في الأيام التي يكون فيها الجو حارًا في الخارج. من ناحية أخرى ، ربما يشتري الناس الآيس كريم ببساطة بمعدل ثابت لأنهم يحبونه كثيرًا.

نبدأ في الإجابة على هذا السؤال من خلال جمع البيانات حول متوسط ​​مبيعات الآيس كريم اليومية وأعلى درجة حرارة يومية. وبالتالي فإن مبيعات الآيس كريم ودرجة الحرارة هما المتغيران اللذان سنستخدمهما لحساب معامل الارتباط.

في بعض الأحيان ، تُسمى بيانات مثل هذه البيانات ثنائية المتغير ، لأن كل ملاحظة (أو نقطة زمنية قمنا فيها بقياس كل من المبيعات ودرجة الحرارة) تحتوي على جزأين من المعلومات يمكننا استخدامها لوصفها. بعبارة أخرى ، نسأل عما إذا كانت مبيعات الآيس كريم ودرجة الحرارة يبدو أنهما يتحركان معًا.

كما كان من قبل ، فإن الطريقة المفيدة لإلقاء نظرة أولية هي استخدام مخطط التشتت:

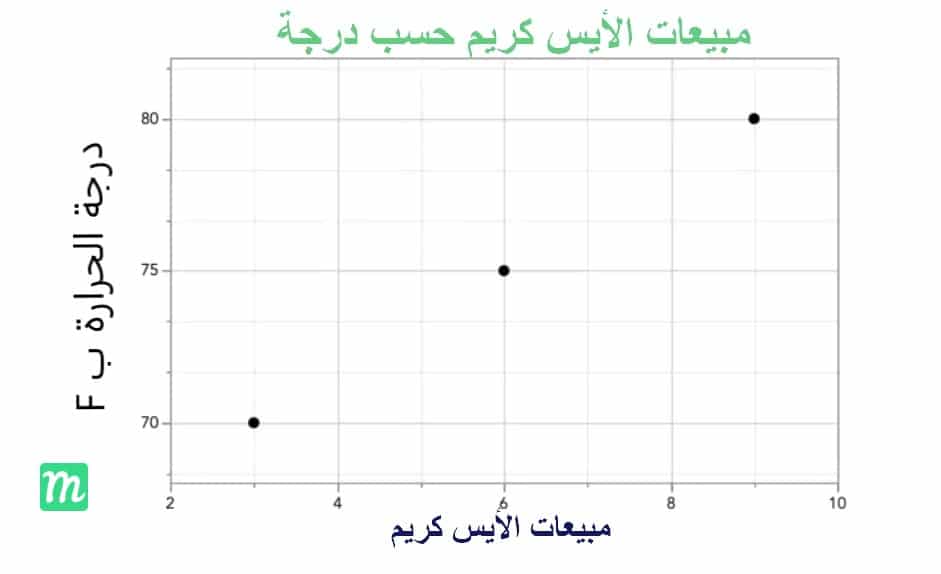
يمكننا أيضًا إلقاء نظرة على هذه البيانات في جدول ، وهو مفيد لمساعدتنا في متابعة حساب المعامل لكل نقطة بيانات. عند الحديث عن البيانات ثنائية المتغير ، من المعتاد استدعاء متغير واحد X والآخر Y (تساعدنا هذه أيضًا في توجيه أنفسنا على مستوى بصري ، مثل محاور الرسم البياني). دعنا نطلق على مبيعات الآي كريم بـ X ودرجة الحرارة Y.

لاحظ أنه تم إقران كل نقطة بيانات. تذكر أننا نبحث حقًا في النقاط الفردية في الوقت المناسب ، ولكل مرة قيمة لكل من المبيعات ودرجة الحرارة.

مبيعات الآي كريم X	درجة الحرارة  F° Y
3	70
6	75
9	80

1.ابدأ بإيجاد وسيلة العينة

الآن بعد أن تم توجيهنا إلى بياناتنا ، يمكننا البدء بحسابين فرعيين مهمين من الصيغة أعلاه: متوسط العينة ، والفرق بين كل نقطة بيانات وهذا يعني (في هذه الخطوات ، يمكنك أيضًا رؤية اللبنات الأساسية للمعيار انحراف).

يتم تمثيل متوسط العينة بالرمزين x̅ و y̅ ، وتسمى أحيانًا “x bar” و “y bar”. يتم حساب متوسطات مبيعات الآيس كريم (x̅) ودرجة الحرارة (y̅) بسهولة على النحو التالي:

2.احسب مسافة كل نقطة بيانات من وسطها

مع وجود المتوسط المتوفر لكل من المتغيرين لدينا ، فإن الخطوة التالية هي طرح متوسط مبيعات الآيس كريم (6) من كل نقطة من نقاط بيانات المبيعات لدينا (xi في الصيغة) ، ومتوسط درجة الحرارة (75) من كل نقطة من نقاط بيانات درجة الحرارة لدينا (yi في الصيغة). لاحظ أن هذه العملية ينتج عنها أحيانًا رقم سالب أو صفر!

3.أكمل الجزء العلوي من معادلة المعامل

يسمى هذا الجزء من المعادلة مجموع المنتجات. المنتج هو رقم تحصل عليه بعد الضرب ، لذا فإن هذه الصيغة هي بالضبط ما يبدو عليه: مجموع الأرقام التي تضربها.

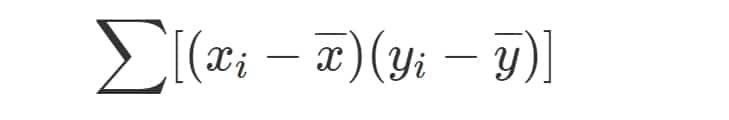
نأخذ القيم المزدوجة من كل صف في آخر عمودين في الجدول أعلاه ، ونضربها (تذكر أن ضرب رقمين سالبين يجعل النتيجة موجبة!) ، ونجمع هذه النتائج:

4.أكمل الجزء السفلي من معادلة المعامل

يبدو مقام معادلة معامل الارتباط كما يلي:

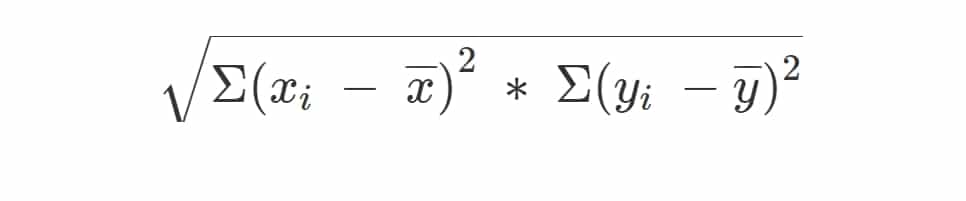
دعنا نتعامل مع التعبيرات في هذه المعادلة بشكل منفصل ونسقط الأرقام من مثال مبيعات الآيس كريم:

عندما نضرب ناتج التعبيرين معًا ، نحصل على: 18×50 = 900

هذا يجعل الجزء السفلي من المعادلة: 900√=30

5.قم بإنهاء الحساب ، وقارن نتيجتنا مع مخطط التشتت

ها هي معادلة معامل الارتباط في الإحصاء الكاملة مرة أخرى:

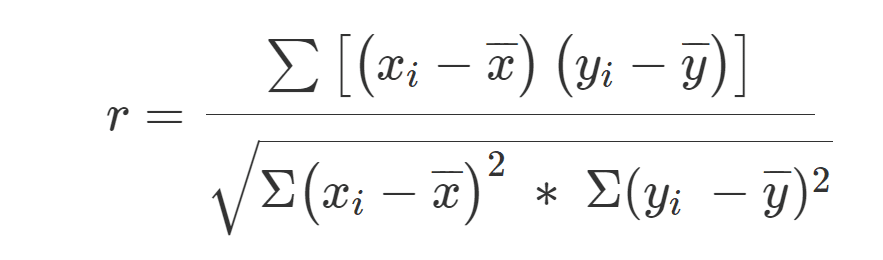
دعنا نسحب أرقام البسط والمقام التي حسبناها أعلاه: r=30/30=1

علاقة تامة بين مبيعات الآيس كريم وأيام الصيف الحارة! بالطبع ، من غير المرجح العثور على ارتباط مثالي في العالم الحقيقي الذي لو كنا نعمل مع بيانات حقيقية ، سنفترض أننا ارتكبنا خطأً للحصول على مثل هذه النتيجة.

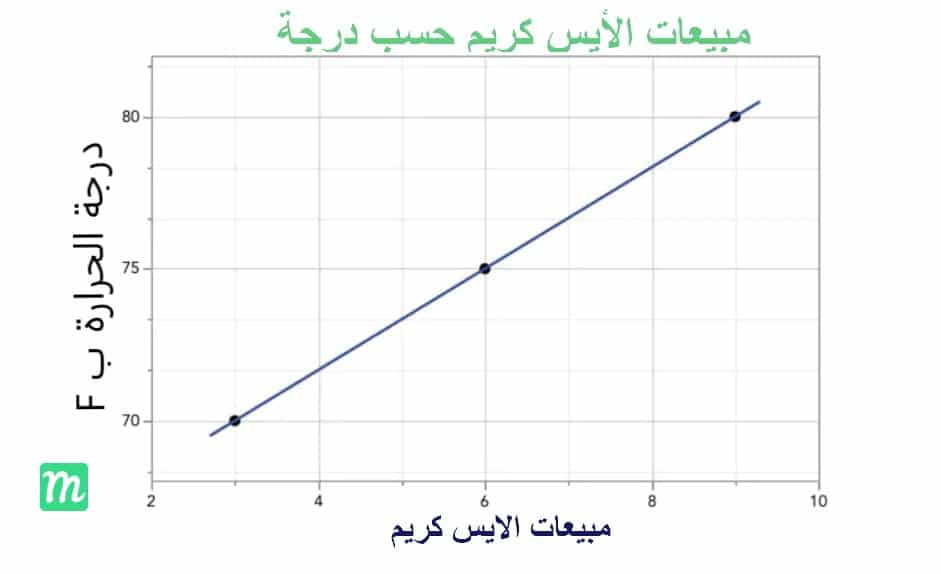
لكن هذه النتيجة من البيانات المبسطة في مثالنا يجب أن يكون لها معنى بديهي بناءً على مجرد النظر إلى نقاط البيانات. دعنا ننظر مرة أخرى إلى مخططنا المبعثر:

تخيل الآن رسم خط من خلال مخطط التشتت. هل ستبدو ملائمة خطية مثالية؟

ما هي بعض القيود التي يجب مراعاتها؟

الارتباط ينظر فقط إلى المتغيرين في متناول اليد ولن يعطي نظرة ثاقبة للعلاقات التي تتجاوز البيانات ثنائية المتغير. لن يكتشف هذا الاختبار (وبالتالي سيتم تشويهه) القيم المتطرفة في البيانات ولا يمكنه اكتشاف العلاقات المنحنية بشكل صحيح.

إحصائيات الارتباط والاستثمار

العلاقة بين متغيرين مفيدة بشكل خاص عند الاستثمار في الأسواق المالية. على سبيل المثال ، يمكن أن يكون الارتباط مفيدًا في تحديد مدى جودة أداء الصندوق المشترك بالنسبة لمؤشره المعياري ، أو صندوق أو فئة أصول أخرى. من خلال إضافة صندوق استثمار مشترك منخفض أو سلبي إلى محفظة قائمة ، يكتسب المستثمر مزايا التنويع.

بعبارة أخرى ، يمكن للمستثمرين استخدام الأصول أو الأوراق المالية المرتبطة بشكل سلبي لتحوط محافظهم وتقليل مخاطر السوق بسبب التقلبات أو التقلبات الشديدة في الأسعار. يقوم العديد من المستثمرين بالتحوط من مخاطر سعر المحفظة ، مما يقلل بشكل فعال من أي مكاسب أو خسائر رأسمالية لأنهم يريدون توزيعات الأرباح أو العائد من الأسهم أو الأوراق المالية.

تسمح إحصائيات الارتباط أيضًا للمستثمرين بتحديد متى تتغير العلاقة بين متغيرين. على سبيل المثال ، عادةً ما يكون لأسهم البنوك ارتباط إيجابي للغاية بأسعار الفائدة ، حيث يتم احتساب معدلات القروض غالبًا بناءً على أسعار الفائدة في السوق.

إذا كان سعر سهم بنك معين ينخفض ​​بينما ترتفع أسعار الفائدة ، يمكن للمستثمرين استخلاص أن هناك شيئًا ما منحرفًا في هذا البنك المحدد. إذا كانت أسعار أسهم البنوك الأخرى في القطاع آخذة في الارتفاع أيضًا ، يمكن للمستثمرين أن يستنتجوا أن انخفاض أسهم البنوك الخارجية لا يرجع إلى أسعار الفائدة.

بدلاً من ذلك ، من المرجح أن يتعامل البنك الضعيف الأداء مع قضية داخلية أساسية.

الأسئلة الشائعة